Fun with Ternary Search（暂未翻译）

This year is my first year doing the Advent of Code challenge, and today (2021 Day 7)'s challenge is a fun one.

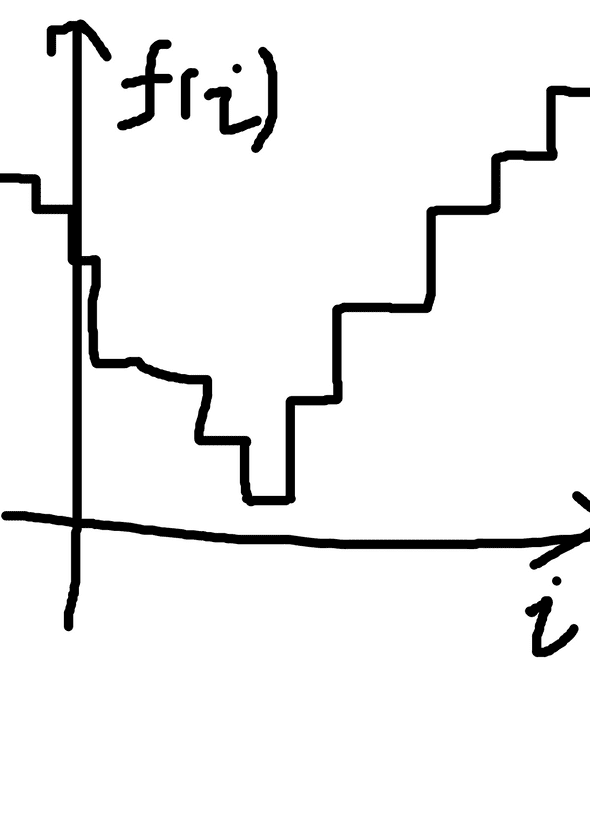
I won't go to the details, but the problem involves finding the minimum for a function. The function takes an integer and returns another integer. An interesting property of that function is that it has one "valley": Everything at the left of the global minimal point monotonically decreases. Everything at the right of the global minimal point monotonically increases.

You can think the function output as a bunch of integers like

100, 81, 56, 32, 16, 33, 44, 78, 129

And we want to find out the value 16.

Naively we can evaluate the function at every point in the domain and then find the minimum, and a slightly better way is to evaluate the function until we find where the result starts to increase. Both strategies requires O(n) time, but since our data are nicely "sorted," we can do better.

Ternary Search

Ternary Search, similar to binary search, expliots our data's pattern, and can achieve O(log n) asymptotic time. Wikipedia describe it as a technique for "finding the minimum or maximum of a unimodal function," which is exactly the function we want to solve. The basic idea is simple: if we partition our domain into three segment by two point: left and right, then we can evaluate the function at left and right and get several cases:

• f(left) < f(right)
• f(left) > f(right)
• f(left) == f(right)

If f(left) < f(right), which means either both left and right points are greater than the position of the local minimum, or left is less than the position of local minimum and right is greater than the position of local minimum. In either case, we know that the local minimum is not at the right hand side of right, so we can discard that part of the domain.

If f(left) > f(right), similarly we can discard the left hand side of left. And if f(left) == f(right), we can discard both side and only keep the range [left, right].

We can equally trisect the domain into left and right, and then we can run the above process recursively or iteratively to solve the problem. We still need a terminate condition: since our left and right can be stuck if right - left <= 2, we stop there and then fall back to linear search. And we can have the following pseudocode:

var left = domain.min
var right = domain.max
while (right - left) > 3 {
  let left_third = left + (right - left) / 3
  let right_third = right - (right - left) / 3

  if f(left_third) < f(right_third) {
    right = right_third
  } else {
    left = left_third
  }
}

for i in left until right get the smallest f(i)

It is an elegent and fun algorithm, and I am suprised that today is the first time I hear about it. And hopefully now you also understand how and when to use this algorithm.